Skillnad mellan medel och median
 Share
Share
 Den centrala tendensen innebär att datapunkterna tenderar att klara kring sitt centrala eller medelstora värde. De två mest använda åtgärderna för central tendens är medelvärde och median. Betyda definieras som det "centrala" värdet av den givna datamängden medan median är "medelvärdet" i den givna uppsättningen data.
Den centrala tendensen innebär att datapunkterna tenderar att klara kring sitt centrala eller medelstora värde. De två mest använda åtgärderna för central tendens är medelvärde och median. Betyda definieras som det "centrala" värdet av den givna datamängden medan median är "medelvärdet" i den givna uppsättningen data.
Ett idealiskt mått på central tendens är en som är tydligt definierad, lättförståelig, enkelt beräknad. Den bör baseras på alla observationer och minst påverkas av extrema observationer i uppsättningen data.
Människor kontrast ofta dessa två åtgärder, men faktum är att de är olika. Denna artikel lyfter särskilt fram de grundläggande skillnaderna mellan medel och median. Ta en titt.
Innehåll: Mean Vs Median
Jämförelsediagram
| Grunder för jämförelse | Betyda | Median |
|---|---|---|
| Menande | Medel hänvisar till det enkla genomsnittet av den givna uppsättningen värden eller kvantiteter. | Median definieras som mittnumret i en ordnad värdeslista. |
| Vad är det? | Det är ett aritmetiskt medelvärde. | Det är positionellt medelvärde. |
| Representerar | Dataöverföringscentrumets tyngdpunkt | Dataöverföringscentrumets tyngdpunkt Mittpunkt för dataset |
| Tillämplighet | Normal distribution | Skewed distribution |
| outliers | Medel är känslig för utjämnare. | Median är inte känslig för outliers. |
| Beräkning | Medel beräknas genom att lägga till alla observationer och sedan dela upp det erhållna värdet med antalet observationer. | För att beräkna median är datasatsen ordnad i stigande eller nedåtgående ordning, då är det värde som faller i exakt mitten av den nya datasatsen, median. |
Definition av medelvärde
Medelvärdet är den allmänt använda mätningen av central tendensen, som definieras som medelvärdet av uppsättningen värden. Den representerar modellen och det vanligaste värdet av det givna värdet. Det kan beräknas, både i diskret och kontinuerlig serie.
Medelvärdet är lika med summan av alla observationer dividerat med antalet observationer i datamängden. Om värdet som antas av en variabel är lika, kommer dess medelvärde också att vara samma. Medel kan vara av två typer, provet betyder (x tj) och populationen medelvärde (μ). Det kan beräknas med given formel:
- Aritmetisk medelvärde:
 där Σ = grekiska bokstaven sigma, betecknar summan av ...
där Σ = grekiska bokstaven sigma, betecknar summan av ...
n = antal värden - För diskret serie:
 var, f = frekvens
var, f = frekvens - För kontinuerliga servies:
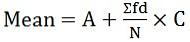 där d = (X-A) / C
där d = (X-A) / C
A = Antaget medelvärde
C = Gemensam divisor
Definition av median
Medianen är ett annat viktigt mått på central tendens, användes för att fördela värdet i två lika delar, dvs större hälften av provet, population eller sannolikhetsfördelning från den nedre halvan. Det är medelvärdet som uppnås när observationerna sorteras i en viss ordning, antingen stigande eller nedåtgående ordning.
För beräkningen av medianen, för det första, ordna observationerna i lägsta till högsta eller högsta till lägsta, använd sedan lämplig formel enligt villkoren nedan:
- Om antalet observationer är udda:
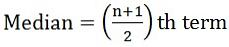 där n = antal observationer
där n = antal observationer - Om antalet observationer är även:
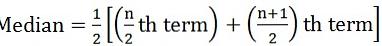
- För kontinuerliga serier:
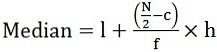 där, l = nedre gränsen för medianklassen
där, l = nedre gränsen för medianklassen
c = kumulativ frekvens för föregående medelklass
f = Medianklassens frekvens
h = klassbredd
Viktiga skillnader mellan medel och median
De signifikanta skillnaderna mellan medel och median finns i artikeln nedan:
- I statistik definieras ett medelvärde som det enkla genomsnittet av den givna uppsättningen värden eller kvantiteter. Medianen sägs vara mitttalet i en ordnad lista över värden.
- Medan medelvärdet är det aritmetiska medelvärdet är medianen lägesgenomsnitt, i huvudsak bestämmer datasetets position medianvärdet av medianen.
- Mean skisserar datasätets tyngdpunkt medan median markerar det mesta värdet av datasatsen.
- Medelvärdet är lämpligt för normalt distribuerad data. I andra änden är median bäst när datafördelningen är skevad.
- Medlet påverkas mycket av det extrema värdet som inte är fallet med en median.
- Medelvärdet beräknas genom att lägga till alla observationer och sedan dela upp det värde som erhållits med antalet observationer. resultatet är medelvärde. I motsats till medianen är datasatsen ordnad i stigande eller nedåtgående ordning, då är det värde som faller i exakt mitten av den nya datasatsen median.
Exempel
Hitta medelvärdet och medianen för den givna uppsättningen data:
58, 26, 65, 34, 78, 44, 96
Lösning: För att beräkna medel måste du dela upp summan av observationer med antalet observationer,

 Medel = 57,28
Medel = 57,28
För att beräkna medianen först och främst ordna serien i en sekvens, d.v.s. lägst till högst,
26, 34, 44, 58, 65, 78, 96
 där n = antal observationer
där n = antal observationer
Slutsats
Efter att ha granskat ovanstående punkter kan vi säga att dessa två matematiska begrepp är olika. Aritmetisk medelvärde eller medel anses vara den bästa mätningen av central tendensen eftersom den innehåller alla funktioner i en idealisk åtgärd men det har en nackdel att provtagningsfluktuationerna påverkar medelvärdet.
På samma sätt är medianen också entydigt definierad och lätt att förstå och beräkna, och det bästa med denna åtgärd är att det inte påverkas av provtagningsfluktuationer, men den enda nackdelen med medianen är att den inte är baserad på alla observationer. För öppen ändeklassificering föredras medianen normalt över genomsnittet.
 där Σ = grekiska bokstaven sigma, betecknar summan av ...
där Σ = grekiska bokstaven sigma, betecknar summan av ... var, f = frekvens
var, f = frekvens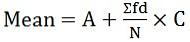 där d = (X-A) / C
där d = (X-A) / C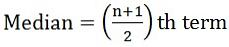 där n = antal observationer
där n = antal observationer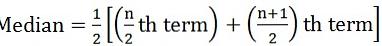
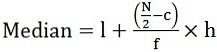 där, l = nedre gränsen för medianklassen
där, l = nedre gränsen för medianklassen Median = 4th termen = 58
Median = 4th termen = 58