Hur man hittar asymptoter av en hyperbola
 Share
Share
Hyperbel
Hyperbolan är en konisk del. Termen hyperbola hänvisas till de två bortkopplade kurvorna som visas i figuren.
Om huvudaxlarna sammanfaller med de kartesiska axlarna är den allmänna ekvationen för hyperbola av formen:

Dessa hyperboler är symmetriska runt y-axeln och är kända som y-axelhyperbola. Den hyperbola symmetriska runt x-axeln (eller x-axel hyperbola) ges av ekvationen,
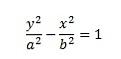 Hur man hittar asymptoter hos en hyperbola
Hur man hittar asymptoter hos en hyperbola
För att hitta asymptoter hos en hyperbola, använd en enkel manipulation av parabolas ekvation.
jag. Först lägg parabolas ekvation till ovan angiven form
Om parabolen ges som mx2+ny2=l, genom att definiera
en= √ (l/m) och b= √ (-l/n) var l<0
(Detta steg är inte nödvändigt om ekvationen ges i standard från.

ii. Därefter ersätt ekvations högra sida med noll.

III. Faktorera ekvationen och ta lösningar

Därför är lösningarna ,

Ekvationer av asymptoter är

Ekvationer av asymptoter för x-axelhyperbolan kan också erhållas med samma förfarande.
Hitta asymptoter av en hyperbola - Exempel 1
Tänk på hyperbolan som ges av ekvationen x2/ 4-y2/ 9 = 1. Hitta ekvationerna för asymptoterna.

Skriv om ekvationen och följ ovanstående procedur.
x2/ 4-y2/ 9 = x2/ 22 -y2/ 32 = 1
Genom att ersätta högra sidan med noll blir ekvationen x2/ 22 -y2/ 32 = 0.
Faktorisering och lösning av ekvationen ger,
(X / 2-y / 3) (x / 2 + y / 3) = 0
Ekvationer av asymptoter är,
3x-2y = 0 och 3x + 2y = 0
Hitta asymptoter av en hyperbola - Exempel 2
- Ekvation av en parabola ges som -4x² + y² = 4

Denna hyperbola är en x-axel hyperbola.
Omarrangering av hyperbolas villkor i standarden från ger
-4x2+ y2= 4 => y2/ 22 -x2/ 12 = 1
Faktorerande ekvationen ger följande
(Y / 2-x) (y / 2 + x) = 0
Därför är lösningarna y-2x = 0 och y + 2x = 0.
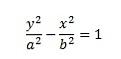 Hur man hittar asymptoter hos en hyperbola
Hur man hittar asymptoter hos en hyperbola 