Hur man beräknar halva livet
 Share
Share
I det här avsnittet kommer vi att lära oss om halveringstiden och härleda formeln för att beräkna halveringstiden. I radioaktivitet, halveringstid är tiden som tas av hälften av radioaktiva kärnor i ett prov av en radioaktiv isotop att förfallna. Antalet radioaktiva kärnor i ett prov faller exponentiellt över tiden. För att beräkna halveringstid används därför matematiken för exponentiell sönderfall. Halvlivet är ett extremt viktigt koncept för tillämpningar av radioaktivitet. Radioisotoper som introduceras till organ i strålbehandling, till exempel, får inte linga långsamt i en patients kropp. Å andra sidan måste isotoper som används för att datera historiska artefakter ha långa halva liv så att tillräckligt med dem har förblev fram till idag för oss att bestämma objektens ålder.
Skillnad mellan slumpmässig och spontan typ av radioaktivt förfall
Radioaktivt förfall kategoriseras som båda slumpmässig och spontan.
- Radioaktivt förfall är slumpmässigt eftersom vi inte kan bestämma när en given kärna kommer att förfallna eller bestämma hur lång tid det tar innan en given kärna skulle förfallna. Följaktligen har varje radioaktiv kärna i ett prov samma sannolikhet för förfall vid en given tidpunkt.
- Radioaktivt förfall är spontant eftersom det inte påverkas av externa förhållanden.
Vad är Half Life
Antalet radioaktiva kärnor i ett prov minskar, eftersom en gång kärnan faller genom alfa-, beta- och gammaförlust kan de inte genomgå samma förfallsprocess igen. Antalet radioaktiva kärnor i provet minskar exponentiellt.
De aktivitet, eller den sönderfallshastighet,är förändringshastigheten av antalet radioaktiva kärnor. Detta ges av,

Det negativa tecknet betyder att antalet radioaktiva kärnor i ett prov är minskande över tid. $ latex \ lambda & s = 1 $ heter sönderfallskonstant. Det ger sannolikheten att en given kärna kommer att sönderfalla per tidsenhet. Förfallskonstanten har ett specifikt värde för vilken som helst given kärnavfallsprocess. Ju högre  , Ju högre sannolikheten för förfall och antalet radioaktiva kärnor i provet minskar snabbare.
, Ju högre sannolikheten för förfall och antalet radioaktiva kärnor i provet minskar snabbare.
Om antalet radioaktiva kärnor i ett prov i taget  är
är  , då antalet radioaktiva kärnor
, då antalet radioaktiva kärnor  i provet efter en tid
i provet efter en tid  ges av:
ges av:

Antalet radioaktiva kärnor i provet minskar exponentiellt. Halva livet ( ) Är den tid som tas för antalet radioaktiva kärnor i tiden att halveras. Om vi ritar en graf om hur antalet radioaktiva kärnor i provet varierar över tid, får vi följande graf:
) Är den tid som tas för antalet radioaktiva kärnor i tiden att halveras. Om vi ritar en graf om hur antalet radioaktiva kärnor i provet varierar över tid, får vi följande graf:

Hur man beräknar halveringstid - radioaktiv sönderfallskurva
Hur man beräknar aktivitet
Aktiviteten hos provet är proportionell mot antalet närvarande radioaktiva kärnor. Så, vi kan göra ett motsvarande uttalande,

var  är provets aktivitet vid tidpunkten
är provets aktivitet vid tidpunkten  , med
, med  aktiviteten när
aktiviteten när  .
.
Om en graf av aktivitet vs tid dras kommer den att producera ett diagram med samma form (dvs aktiviteten försvinner också exponentiellt).
Aktiviteten mäts med SI-enheten becquerel (Bq). En aktivitet på 1 Bq motsvarar en hastighet av 1 sönderfall per sekund. De curie (Ci) är en annan enhet som används för att mäta aktivitet. 1 Ci = 3,7 × 1010 bq.
Half Life Formula
Vi kommer nu att härleda en formel för att få halveringstiden från förfallet konstant. Vi börjar med,

Efter en tid  , antalet radioaktiva kärnhalvor. Så,
, antalet radioaktiva kärnhalvor. Så,  , eller
, eller

Med båda sidornas naturliga logaritmen får vi:

och så,

Hur man beräknar halva livet
Exempel 1
Indium-112 har en halveringstid på 14,4 minuter. Ett prov innehåller 1,32 × 1024 atomer av indium-112.
a) Hitta nedbrytningen konstant
b) Ta reda på hur många atomer av indium-112 som skulle lämnas i provet efter 1 timme.
a) Sedan  ,
,

b) Användning  ,
,  atomer.
atomer.
Exempel 2
Under en behandling för sköldkörtelcancer ges en patient ett prov av jod-131 som ska intagas, vilket har en aktivitet på 1,10 MBq. Halvlivet av jod 131 är 8,02 dagar. Hitta aktiviteten av jod-131 i patientens kropp efter 5 dagars intag.
Vi använder  . Först arbetar vi ut
. Först arbetar vi ut  :
:

Sedan,
 MBq.
MBq.
Notera:
- Vi beräknade direkt sönderfallskonstanten per dag och behöll halveringstiden också i dagar. Så dagarna avbröt när vi beräknade
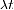 och det var inte nödvändigt att konvertera tider till sekunder (det skulle ha fungerat också, men det skulle ha inneburit lite mer beräkning)
och det var inte nödvändigt att konvertera tider till sekunder (det skulle ha fungerat också, men det skulle ha inneburit lite mer beräkning) - I verkligheten skulle aktiviteten vara mindre. Detta beror på att det också finns ett biologiskt halveringstid i samband med aktiviteten. Detta är den takt som patienten utsöndrar radioaktiva kärnor från deras kropp.
Exempel 3
Beräkna halveringstiden för en radioaktiv isotop vars aktivitet minskar med 4% över 1000 år.
4% = 0,04. Vi har nu
 . Med ln på båda sidor,
. Med ln på båda sidor,
 per år.
per år.
 216 år.
216 år.
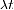 och det var inte nödvändigt att konvertera tider till sekunder (det skulle ha fungerat också, men det skulle ha inneburit lite mer beräkning)
och det var inte nödvändigt att konvertera tider till sekunder (det skulle ha fungerat också, men det skulle ha inneburit lite mer beräkning)