Skillnad mellan T-test och ANOVA
 Share
Share
 Det finns en tunn avgränsning mitt mellan t-test och ANOVA, dvs när man endast ska jämföra populationen av endast två grupper, t-test används, men när medel för mer än två grupper ska jämföras, ANOVA Är föredraget.
Det finns en tunn avgränsning mitt mellan t-test och ANOVA, dvs när man endast ska jämföra populationen av endast två grupper, t-test används, men när medel för mer än två grupper ska jämföras, ANOVA Är föredraget.
T-test och Variansanalys förkortad som ANOVA, är två parametriska statistiska tekniker som används för att testa hypotesen. Eftersom dessa är baserade på det gemensamma antagandet att den befolkning från vilken provet ritas bör normalt fördelas, homogenitet av varians, slumpmässig provtagning av data, observationernas oberoende, mätning av den beroende variabeln på förhållandet eller intervallnivå, misstolkar personerna ofta dessa två.
Här är en artikel som presenteras för dig att förstå den signifikanta skillnaden mellan t-test och ANOVA, ta en titt.
Innehåll: T-test Vs ANOVA
Jämförelsediagram
| Grunder för jämförelse | T-test | ANOVA |
|---|---|---|
| Menande | T-test är ett hypotesprov som används för att jämföra medel för två populationer. | ANOVA är en statistisk teknik som används för att jämföra medel från mer än två populationer. |
| Teststatistik | (x ̄-μ) / (s / nn) | Mellan provvariationen / inom provvariationen |
Definition av T-test
T-testet beskrivs som det statistiska testet som undersöker huruvida populationen av två prover skiljer sig väsentligt från varandra, med användning av t-distribution som används när standardavvikelsen inte är känd och provstorleken är liten. Det är ett verktyg för att analysera om de två proverna dras från samma befolkning.
Testet är baserat på t-statistik, vilket förutsätter att variabeln normalt distribueras (symmetrisk klockformad fördelning) och medelvärdet är känt och populationsvariation beräknas från provet.
I t-test tar null hypotes form av H0: μ (x) = μ (y) mot alternativ hypotes H1: μ (x) ≠ μ (y), där μ (x) och μ (y) representerar populationen. Graden av frihet för t-test är n1 + n2 - 2
Definition av ANOVA
Analys av varians (ANOVA) är en statistisk metod som vanligen används i alla de situationer där en jämförelse ska göras mellan mer än två populationer, som utbytet av grödan från flera frövarianter. Det är ett viktigt analysverktyg för forskaren som gör det möjligt för honom att genomföra test samtidigt. När vi använder ANOVA antas att provet dras från den normalt distribuerade befolkningen och populationsvariationen är lika.
I ANOVA delas den totala variationen i en dataset i två typer, dvs mängden allokerad till chans och mängd som tilldelas särskilda orsaker. Dess grundläggande princip är att testa variationerna bland befolkningsmedel genom att bedöma variationen inom gruppposter, proportionellt med variationen mellan grupper. Inom provet är variansen på grund av den slumpmässiga oförklarliga störningen medan olika behandling kan orsaka mellan provvariationen.
Med hjälp av denna teknik testar vi nollhypotesen (H0) där alla befolkningsorgan är samma eller alternativa hypoteser (H1) vari åtminstone en populationsmedel är annorlunda.
Viktiga skillnader mellan T-test och ANOVA
De signifikanta skillnaderna mellan T-test och ANOVA diskuteras i detalj i följande punkter:
- Ett hypotesprov som används för att jämföra medel för två populationer kallas t-test. En statistisk teknik som används för att jämföra medel från mer än två populationer kallas Analys av Varians eller ANOVA.
- Teststatistik för T-test är:
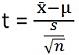 Teststatistik för ANOVA är:
Teststatistik för ANOVA är: 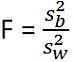
Slutsats
Efter att ha granskat ovanstående punkter kan man säga att t-test är en speciell typ av ANOVA som kan användas när vi bara har två populationer för att jämföra deras medel. Även om risken för fel kan öka om t-test används när vi måste jämföra mer än två medel för populationerna samtidigt, är det därför ANOVA används
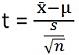 Teststatistik för ANOVA är:
Teststatistik för ANOVA är: