Skillnad mellan sekvens och serie

I matematik och statistik är linjen som avgränsar sekvens och serie tunna och suddiga, på grund av vilka många tycker att dessa termer är en och samma sak. Ändå skiljer sig begreppet från sekvens från serie i den meningen att sekvens hänvisar till ett arrangemang i den särskilda ordningen i vilken relaterade termer följer varandra, dvs den har en identifierad första enhet, andra enhet, tredje enhet och så vidare.

När en sekvens följer en viss regel kallas den som progression. Det är inte exakt samma som serier som definieras som summeringen av elementen i en sekvens. Ta en läs av artikeln för att få veta den signifikanta skillnaden mellan sekvens och serie.

Innehåll: Sequence Vs Series

Jämförelsediagram

Grunder för jämförelse	Sekvens	Serier
Menande	Sekvens beskrivs som uppsättningen tal eller objekt som följer ett visst mönster.	Serien hänvisar till summan av elementen i sekvensen.
Ordning	Viktig	Ibland viktigt
Exempel	1, 3, 5, 7, 9, 11 ... n ...	1 + 3 + 5 + 9 + 11 ... n ...

Definition av sekvens

I matematik, en ordnad uppsättning objekt eller siffror, som a₁, en₂, en₃, en₄, en₅, en₆... a_{n ... .}sägs vara i en sekvens, om, enligt bestämd regel, har ett bestämt värde. Medlemmarna i sekvensen kallas term eller element som är lika med vilket värde som helst av det naturliga numret. Varje term i en sekvens är relaterad till föregående och efterföljande term. I allmänhet har sekvenser en dold regler eller ett mönster som hjälper dig att ta reda på värdet av nästa term.

Den n: e termen är funktionen av heltal n (positiv), betraktad som sekvensens allmänna term. En sekvens kan vara ändlig eller oändlig.

Finite Sequence: En ändlig sekvens är en som slutar i slutet av listan med nummer a₁, en₂, en₃, en₄, en₅, en₆... a_n, representeras av:
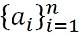
Oändlig sekvens: En oändlig sekvens hänvisar till en sekvens som är oändlig, a₁, en₂, en₃, en₄, en₅, en₆... a_{n ... .}., representeras av:

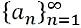
Definition av serie

Tillägget av villkoren i en sekvens (a_n), är känd som serie. Serie kan som sekvens också vara ändlig eller oändlig, där en ändlig serie är en som har ett begränsat antal termer skrivna som en₁+ en₂+ en₃ + en₄+ en₅ + en_{6 +}... a_n. Till skillnad från oändliga serier, där antalet element inte är ändliga eller som är oändliga, skrivs som en₁+ en₂+ en₃ + en₄+ en₅ + en_{6 +}... a_n+_{... .}

Om en₁+ en₂+ en₃ + en₄+ en₅ + en_{6 +}... a_n = S_n, sedan S_n betraktas som summan till n delar av serien. Summen av termer representeras ofta av grekiska bokstaven sigma (Σ). Därav,

Viktiga skillnader mellan sekvens och serie

Skillnaden mellan sekvens och serie kan dras tydligt av följande skäl:

Sekvensen definieras som samling av nummer eller objekt som följer ett bestämt mönster. När elementen i sekvensen läggs till tillsammans är de kända som serier.
Beställa frågor i en sekvens, eftersom det finns en viss regel som föreskriver sekvensens mönster. Därför är 1, 2, 3three annorlunda än 3, 1, 2. Å andra sidan, i en serieordning av utseende kan eller inte spelar någon roll, precis som i fallet med absolut konvergent serie spelar ingen roll upp ordningen. Så, 1 + 2 + 3 är samma som 3 + 1 + 2, endast deras sekvens är olika.

Slutsats

Aritmetisk Progression (A.P.) och Geometric Progression (G.P.) är också sekvenser, inte serier. Aritmetisk Progression är en sekvens där det finns en gemensam skillnad mellan de på varandra följande termerna, såsom 2, 4, 6, 8 och så vidare. Tvärtom, i en geometrisk progression, är varje element i sekvensen den gemensamma multipeln av föregående term, såsom 3, 9, 27, 81 och så vidare. På liknande sätt är Fibonacci Sequence också en av de populära oändliga sekvenserna, där varje term erhålles genom att lägga till de två föregående termerna 1, 1, 3, 5, 8, 13, 21 och så vidare.

Utbildning