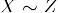Skillnad mellan lika och ekvivalent
 Share
Share
Huvudskillnad - lika vs. ekvivalent
Lika och likvärdig är termer som används ofta i matematik. De huvudskillnad mellan lika och ekvivalent är det termen lika hänvisar till saker som liknar alla aspekter, medan termen ekvivalent avser saker som liknar en viss aspekt. Observera att i uppsättningsteori, orden "lika" och "ekvivalent" har särskilda betydelser, vilket vi kommer att se nedan.
Vad betyder lika betydelse
I allmänhet är två saker lika om de är lika i alla avseenden.
När det gäller setteori är två uppsättningar lika om de båda innehåller samma element. De ordning där de är listade i en uppsättning spelar ingen roll. Antag exempelvis
 och
och
 sedan,
sedan,
uppsättningen  är lika med uppsättningen
är lika med uppsättningen  .
.
Vad betyder ekvivalent
Två saker kan sägas vara likvärdiga om de liknar under ett visst tillstånd. Därför, om två enheter är likvärdig till största delen beror under förutsättning att vi använder för att beskriva deras likvärdighet. Exempelvis är siffrorna 2 och 7 ekvivalenta i den meningen att de båda är primtal. Men om villkoret vi är intresserade av är att ta reda på om siffrorna är jämn, så är det i denna mening 2 och 7 inte likvärdig. Vi använder symbolerna  eller
eller  för att ange det
för att ange det  och
och  är ekvivalenta.
är ekvivalenta.
När ett kriterium har definierats uppfyller saker som motsvarar ekvivalensrelationer:
- reflexivitet:
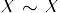
- Symmetri: Om
 , sedan
, sedan 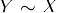
- Transitivity: Om
 och
och 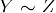 , sedan
, sedan 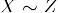
I uppsättningsteori är två uppsättningar likvärdig om de har samma antal element. Elementen själva behöver inte vara samma heller, endast Antalet element måste vara detsamma. Antag exempelvis
 och
och
 sedan,
sedan,
uppsättningarna  och
och  är ekvivalenta.
är ekvivalenta.

Symboler för att uttrycka jämlikhet och ekvivalens
Skillnad mellan lika och ekvivalent
Allmänna meningar
När två saker är lika, De är lika i alla aspekter.
När saker är likvärdig, De liknar en viss aspekt.
I uppsättningsteori
När två uppsättningar är lika, de innehåller samma element.
När två uppsättningar är likvärdig, de innehåller samma antal element.
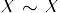
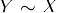
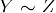 , sedan
, sedan