Skillnad mellan Laplace och Fourier Transforms

Laplace vs Fourier Transforms
 

Både Laplace transform och Fourier transform är integrerade transformationer, som oftast används som matematiska metoder för att lösa matematiskt modellerade fysiska system. Processen är enkel. En komplex matematisk modell omvandlas till en enklare, lösbar modell med en integrerad transformation. När den enklare modellen är löst tillämpas den inversa integrerade transformen, vilket skulle ge lösningen till den ursprungliga modellen.

Till exempel, eftersom de flesta fysiska systemen leder till differentialekvationer, kan de omvandlas till algebraiska ekvationer eller till lägre grad lättlösbara differentialekvationer med hjälp av en integrerad transformation. Då blir problemet enklare.

Vad är Laplace-transformen?

Givet en funktion f (t) av en reell variabel t, dess Laplace-transformation definieras av integralet 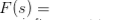(när det existerar), vilket är en funktion av en komplex variabel s. Det betecknas vanligen av L f (t). Den omvända Laplace-transformen av en funktion F(s) anses vara funktionen f (t) på ett sådant sätt att L f (t) = F(s), och i den vanliga matematiska notationen skriver vi, L ^-1F(s) = f (t).Den inverse transformen kan göras unik om nullfunktioner inte är tillåtna. Man kan identifiera dessa två som linjära operatörer definierade i funktionsutrymmet, och det är också lätt att se det, L ^-1L f (t) = f (t), om nullfunktioner inte är tillåtna.

I följande tabell visas Laplace-transformationerna av några av de vanligaste funktionerna.

Vad är Fourier-transformen?

Givet en funktion f (t) av en reell variabel t, dess Laplace-transformation definieras av integralet 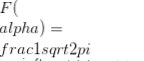(när den existerar), och betecknas vanligtvis av F f (t). Den inverse transformen F ^-1F(α) ges av integralet . Fouriertransformationen är också linjär och kan betraktas som en operatör definierad i funktionsutrymmet.

Med hjälp av Fourier-transformen kan den ursprungliga funktionen skrivas enligt följande förutsatt att funktionen endast har begränsad antal diskontinuiteter och är helt integrerbar.

Vad är skillnaden mellan Laplace och Fourier Transforms?

• Fourier-transformation av en funktion f (t) är definierad som 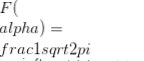, medan laplace-transformen av den definieras vara .
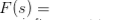• Fourier-transformen definieras endast för funktioner som definieras för alla reella tal, medan Laplace-transformen inte kräver att funktionen definieras för att ställa in de negativa reella tal.
• Fourier-transform är ett speciellt fall av Laplace-transformen. Det kan ses att båda sammanfaller för icke-negativa reella tal. (dvs ta s i Laplace att vara iα + β var α och β är verkliga sådana e ^β= ¹/_{√ (2ᴫ)})
• Varje funktion som har en Fourier-transform kommer att ha en Laplace-transform, men inte vice versa.